Questo “post”, con il medesimo titolo, è stato inserito anche nel forum sugli oggetti GDL
http://www.archiradar.it
Gli artisti italiani del Rinascimento rivoluzionarono il concetto di infinito (∞), come mi spiegò a suo tempo l’emerito professor Pietro Lenzini dell’Accademia di belle Arti di Bologna, forse l’ultimo pittore di pale d’altare esperto di prospettiva scenica. Bologna, nel passato, con i Bibiena, aveva una scuola di prospettiva invidiata da tutta l’Europa. Ancora oggi si studiano e si traducono all’estero le opere del Bibiena, come ho constatato nel visitare un sito spagnolo. A Bologna, dove sono conservati i testi originali, questi rimangono impolverati in biblioteca. Poi non sono disponibili copie. Veramente qui in Italia non si investe nulla nella cultura, credendo in questo modo di operare risparmi, in realtà si sprecano le nostre potenzialità. Si dissipa il nostro patrimonio, poi si piange sopra una crisi dovuta principalmente ad ignoranza, avidità e appunto a spreco.
Tramite il concetto di punto di fuga, si passò dall’infinito potenziale all’infinito attuale. Oggi si tende a trascurare la prospettiva proprio nelle scuole deputate alle arti visive, mentre paradossalmente nelle facoltà di architettura-ingegneria si è ritornati al disegno prospettico realizzato a mano. Infatti la prospettiva si apprende con il disegno, non con il rendering automatico del computer. Il computer non fa errori in termini di geometria, ma dal punto visivo sì. Un allievo mi presentò il rendering prospettico freddo ed esatto di una stanza un po’ squallida, con sul pavimento la proiezione luminosa della finestra aperta. Le ombre di contorni piani su un piano, sono applicazioni del concetto di omologia o di prospettività, se il centro è proprio. A voler essere precisi l’omologia nasce da una prospettività, ove si sovrappongono i due piani di proiezione, che nella prospettività rimangono distinti. L’omologia era esatta, ma quell’ombra proiettata dalla finestra sullo sfondo era assurda. Infatti si restringeva verso l’osservatore invece di dilatarsi.
La prospettiva dunque, come le sue applicazioni, utilizza l’infinito come concetto attuale, per cui punti propri e impropri possono scambiarsi. Per il calcolatore l’infinito semplicemente non esiste. Come fare dunque per rappresentare curve infinite? Basta proiettarle in modo da renderle finite. Questo metodo può servire pure per studiare la forma delle curve e per generarne nuove.
Il disegno a mano è unico e irripetibile, ma è pure approssimativo. L’interfaccia intuitiva del computer aiuta a generare linee complesse, dove la mano interagisce con il calcolo. Tuttavia una curva geometrica, generata da una equazione ha una semplicità e una regolarità che non possiedono le curve disegnate. Gli architetti dovrebbero tenerne conto.
La prospettività si può dunque considerare come un caso di proiezione prospettica tra due piani effettuata da un punto di vista. Su un piano si disegna un forma, poi questa viene proiettata dal centro, esterno al piano, su di un altro piano. Proiettando o ribaltando i due piani uno sull’altro, si ha l’omologia. Un caso di omologia è la prospettiva di un pavimento, con il suo ribaltamento lungo la linea di terra, che corrisponde all’asse dei punti uniti dell’omologia. Se si collegano con rette i punti corrispondenti del pavimento ribaltato e della sua prospettiva, i collegamenti vanno a concorrere in un unico punto che è il centro dell’omologia. Questo centro si può considerare come la proiezione o il ribaltamento sul quadro del punto di vista.
Dato che l’omologia nasce storicamente e logicamente dalla prospettiva, consideriamo i due piani come ortogonali, uno è il pavimento PO l’altro il quadro trasparente PV. Sia h l’altezza dell’osservatore su PO e d la sua distanza da PV. La linea di intersezione LT tra i due piani è l’asse x dell’omologia, l’asse y è la verticale posta di fronte all’osservatore, per cui il punto di fuga principale ha coordinate (0,h). Chiamiamo asse y anche il ribaltamento di y sul pavimento PO. Per evitare confusione nelle formule aggiungiamo un apostrofo alle coordinate relative ai punti giacenti su PV o quadro.
Un punto (x’,y’) su PV viene pertanto proiettato su PO in (x,y)
Formula (1) per ricavare la forma oggettiva sul pavimento dell’oggetto disegnato in prospettiva sul quadro:
x= h*x’/(h-y’)
y= d*x’/(h-y’)
Da notare che per y’=h il denominatore si annulla, perché il punto prospettico si trova sull’orizzonte LO e il suo corrispondente è un punto improprio. In questo caso si tratterebbe di un punto di fuga.
Formula (2) per ricavare la prospettiva sul quadro della forma oggettiva sul pavimento:
x’= d*x/(d+y)
y’= h*y/( d+y)
In questo caso il denominatore si annulla per y=-d, perché il punto oggetto si trova sul piano proiettante parallelo al quadro. Questi punti dello spazio, posti ad un angolo di visuale di 90°, non possono essere rappresentati sul quadro.
Il problema nel tradurre in uno script forme di estensione infinita, nasce, come si è detto, dal fatto che il computer non può riconoscere il concetto di infinito attuale, ma solo quello di infinito potenziale, inteso come possibile aumento del valore di parametro. Supponiamo di voler suddividere l’asse y su PO in modo che punti corrispondenti su PV siano equidistanti.
L’asse y’ su PV avrebbe questa suddivisione dal basso verso la linea d’orizzonte a quota h:
for i=0 to m
y’=h/m*i
next i
Applicando la formula (1) si ricava:
for i=0 to m-1 !formula (3)
y=d*i/(m-i)
next i
Naturalmente bisogna escludere l’ultima coordinata, con m=1, che corrisponde a y’=h.
La distanza tra i punti di questa successione aumenta con progressione geometrica, in modo che si annulla poi sul quadro la riduzione prospettica, per cui i punti appaiono equidistanti.
Però a noi non interessa tanto suddividere l’asse y di PO, ma piuttosto l’asse x.
Infatti una curva su PO si esprime solitamente con y=y(x) e non con x=x(y). Se la curva ha estensione infinita anche in orizzontale non potremo trasformarla con l’omologia nella sua interezza, se non riusciamo a comprimere l’asse x.
Applicando anche per l’asse x una formula analoga alla (3) si ricava:
for i=1 to 2*m-1 !formula (4)
x=p/2*(i-m)*( (1-sgn(i-m))/i + (1+sgn(i-m))/(2*m-i) )
next i
La formula è più complessa perché comprende anche il semiasse negativo, per cui in realtà è divisa in due parti, che si annullano ove conviene tramite sgn(i-m) che vale -1 per i<m e 1 per i>m. Inoltre si è sostituito d con p, dato che la suddivisione di x è indipendente dall’asse y. Con valori di p alti i vertici scorrono verso gli estremi, cioè nella trasformata verso i punti di fuga: con valori bassi aumenta la risoluzione della parte inferiore della curva prospettica
Per verificare se i risultati sono corretti, prima applichiamo la (3) ad una parabola:
y=x^2
x=sqr(y)
La parabola si chiude all’infinito, per cui il suo punto di fuga è il punto principale (0,h)
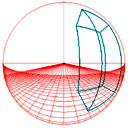
Lo script seguente dovrebbe generare non la parabola, ma una semiellisse tangente alla LO.
h=2
d=2
m=36
for i=0 to m-1
y=d*i/(m-i)
x=sqr(y)
xx= d*x/(d+y) !formula (2): dal PO al PV
yy= h*y/( d+y)
put xx,yy
next i
put 0, h !punto di fuga
poly2 nsp/2, 1+4 , get (nsp)
Utilizziamo ora una iperbole con vertici sull’asse y per verificare i risultati della formula (4)
y=b/a*sqr(a^2+x^2)-d
Il centro dell’iperbole deve essere sul piano proiettante parallelo al quadro PV, altrimenti si ha una porzione di ellisse inferiore alla metà
Lo script è il seguente:
a=1
b=2
h=2
d=2
p=1
m=36
put -d*a/b, h !punto di fuga sinistro
for i=1 to 2*m-1 !formula (4)
x=p/2*(i-m)*( (1-sgn(i-m))/i + (1+sgn(i-m))/(2*m-i) )
y=b/a*sqr(a^2+x^2)-d
xx= d*x/(d+y) !formula (2): dal PO al PV
yy= h*y/( d+y)
put xx,yy
next i
put d*a/b, h !punto di fuga destro
poly2 nsp/2, 1, get (nsp)
A questo punto qualcuno si chiederà: a cosa serve questa complicazione. Forse mi domanderebbe: non avremmo fatto prima a costruire subito una ellisse? Che bisogno c’era di costruire parabole o iperboli per avere ellissi? La risposta è in un film di Stanlio e Ollio, dove sono travestiti da scolaretti con il classico cono di cartone e le orecchie da asino. La cultura, lo studio, non ha solo fini pratici, questo lo insegnavano già gli antichi greci e dovrebbe insegnarlo la scuola. Ogni materia, compresa la geometria e la matematica, hanno in sé una bellezza che prescinde dal suo utilizzo: “Fatti non foste per esser come bruti!” scriveva Dante. La tecnologia va avanti, ma i comportamenti sociali sembrano andare all’indietro: per certi versi ci stiamo comportando come trogloditi. Al posto della musica che ha raggiunto i suoi livelli più raffinati nel 1800, si picchia con il bastone su fusti di benzina, si circola mezzi nudi pieni di tatuaggi e con anelli al naso, non si dipingono quasi più pale d’altare ma si produce merda d’artista, anche se inscatolata, e questo non è certo il peggio. Almeno i nostri avi cavernicoli hanno rispettato la natura, permettendoci di essere ancora qui.
Le curve coniche sono le uniche curve algebriche che si trasformano una nell’altra mediante trasformazioni proiettive come l’omologia. Inoltre sono semplici da costruire direttamente. Quando si passa ad ordini superiori, come per le cubiche o per curve di ordine maggiore, si creano diverse famiglie di curve all’interno del medesimo ordine. Soltanto all’interno di una stessa famiglia è possibile ricavare una curva dall’altra mediante proiezioni, ma non è possibile ottenere in questo modo gli altri tipi. Inoltre le curve del terzo e quarto ordine possono essere sghembe. Le coniche sono sempre piane.
Le curve del quarto ordine si studiano normalmente nei corsi di disegno geometrico, in quanto alcuni tipi si possono ottenere dalle intersezioni di cilindri rotondi.
Costruire una equazione traducibile nel linguaggio GDL di una curva chiusa del quarto ordine è piuttosto complesso. E’ possibile farlo per curve con assi di simmetria, altrimenti l’equazione non si risolve rispetto a una variabile. Si creano infatti equazioni di terzo e quarto grado, anche solo nel cercarne le intersezioni con gli assi. La soluzione algebrica di questi tipi di equazioni fu fornita già nel 1500 da Scipione dal Ferro e credo da Tartaglia, ma poi occorre scomodare i numeri complessi e la soluzione effettiva può essere data solo per approssimazioni. I numeri complessi richiedono qui di risolvere la trisecazione di un arco, salvo casi particolari. La trisecazione di un arco è un problema che ha assillato per generazioni gli antichi matematici e non si risolve in modo elementare, come la quadratura del circolo. Oltre il secondo grado le cose si complicano parecchio. Occorre studiare vie traverse, come appunto la deformazione proiettiva.
La curva algebrica del quarto ordine più semplice è la parabola di ordine 4, ottenuta eguagliando a y un polinomio di grado 4.
La sua forma più elementare presenta il solo monomio di grado 4:
y=a1*x^4
ma non è una curva interessante, essendo un semplice arco come la parabola comune.
Vogliamo allora creare una ammaccatura aggiungendo un monomio di grado 2 con segno negativo:
y= a1*x^4- a2*x^2
A questo punto vediamo il risultato:
a1=.5
a2=1
h=3
d=5
p=1
m=90
for i=1 to 2*m-1 !formula (4)
x=p/2*(i-m)*( (1-sgn(i-m))/i + (1+sgn(i-m))/(2*m-i) )
y= a1*x^4- a2*x^2
xx= d*x/(d+y) !formula (2): dal PO al PV
yy= h*y/( d+y)
put xx,yy
next i
put 0, h !punto di fuga unico
poly2 nsp/2, 1+4, get (nsp)
La curva ha la forma di una lancia o di un cuore rovesciato.
Aumentando a2 rispetto a1 aumenta la divaricazione e la lunghezza delle protuberanze inferiori, ma a2 non può essere aumentato troppo, perché rischia di portare la curva sotto i piedi dell’osservatore, dove si creerebbero punti impropri, con messaggio di errore.
Aumentando a1 rispetto a2 diminuisce l’effetto dell’ammaccatura che scompare per a1=0
Aumentando a1 la curva si stringe e con valori bassi si allarga. Questo perché a1 è legato alla pendenza della curva, che cresce con valori alti.
Dato che la curva si chiude all’infinito, dal punto di vista geometrico LO risulta tangente alla sua trasformata, anche se visivamente non è chiaro per la forma appuntita.
Applicando a questa curva una omologia non più sull’asse y , ma lungo l’asse x e in senso inverso, si crea una asimmetria. La formula (1) viene corretta in questo modo nella formula (5):
x= d*x’/(h-x’) !formula (5): dal PV al PO
y= h*y’/(h-x’)
Questa operazione crea un asse limite in corrispondenza della retta di equazione x’=h, portando all’infinito i rispettivi punti e trascinando tutti gli altri. Quelli posti sull’asse y non si muovono,
Non essendo però in grado di calcolare la larghezza della curva e quindi la distanza appropriata per evitare la creazione di punti impropri, occorre procedere per tentativi con valori di h alti, ovvero occorre visionare la curva precedente per porre l’asse limite alla sua destra.
a1=1
a2=1
h=1 !altezza omologia su y
d=2 !distanza omologia su y
hx=3 !altezza omologia su x, posizione nuovo asse limite
dx=2 !distanza omologia su x
p=1 !la variabile p può coincidere con d oppure no, fa variare le distanze relative fra i punti
m=36
for i=1 to 2*m-1 !formula (4)
x=p/2*(i-m)*( (1-sgn(i-m))/i + (1+sgn(i-m))/(2*m-i) )
y= a1*x^4- a2*x^2
xx= d*x/(d+y) !formula (2): dal PO al PV
yy= h*y/( d+y)
xp= dx*xx/(hx-xx) !formula (5): dal PV al PO
yp= hx*yy/(hx-xx)
put xp ,yp
next i
put 0, h !punto di fuga unico , non si sposta perché sull’asse y
poly2 nsp/2, 1, get (nsp)
Le curve del terzo ordine, come tutte le curve algebriche di ordine dispari, compresa la retta, si chiudono soltanto all’infinito, subendo una torsione a causa del fatto che il piano improprio presenta una sola faccia come il nastro di Moebius. Pertanto non possono chiudersi, nella loro interezza, nel piano euclideo, a differenza delle curve algebriche pari. Tuttavia è possibile considerarne solo una parte.
Come esempio consideriamo la funzione algebrica fratta:
y=1/( a^2-x^2)
è una curva del terzo ordine, costituita da due archi esterni simmetrici a forma di iperbole e di una curva compresa tra due asintoti di equazione x=a e x=-a. Le iperboli esterne puntano all’infinito in basso, mentre la parabola schiacciata intermedia punta all’infinito verso l’alto, con la convessità verso il basso. Il suo massimo relativo è sull’asse x, con ordinata y=1/(a^2).
Per averla tangente all’asse x la abbassiamo:
y=1/( a^2-x^2)- 1/(a^2)
In questo caso x varia semplicemente nell’intervallo [-a,a].
La trasformata omologica della porzione di curva del terzo ordine è generata dallo script:
h=2
d=3
m=36
a=1
for i=1 to m-1
x=2*a/m*i-a
y=1/( a^2-x^2)- 1/(a^2)
xx= d*x/(d+y) !formula (2): dal PO al PV
yy= h*y/( d+y)
put xx,yy
next i
put 0, h !punto di fuga
poly2 nsp/2, 1+4 , get (nsp)
Il risultato è una goccia o un petalo. Il motivo è dovuto al fatto che il punto improprio è un cappio, infatti la curva dovrebbe proseguire. In questo caso LO non è tangente nel punto di fuga.
Infine consideriamo il seguente caso:
data la funzione y=y(x) di cui consideriamo definita la parte entro l’intervallo [0, ∞],
vogliamo comprimerla tramite l’omologia entro un intervallo [0,h]. In questo caso si tratta di realizzarne la prospettività su PV, considerando la curva iniziale come tracciata su PO. Quindi occorre servirsi della formula (2), scambiando gli assi x e y, per cui otteniamo l’inversa della formula (5).
x’= h*x/( d+x) !formula (6): dal PO al PV
y’= d*y/(d+x)
Inoltre le suddivisioni su x+ devono allargarsi secondo la progressione geometrica, per avere una distribuzione uniforme dei punti nella trasformata omologica (altrimenti si accumulerebbero in vicinanza di x=0 e si diraderebbero verso x=h).
Lo script finale è il seguente:
h=2
d=2
a=1
k=1
p=2 !valore dell’intervallo, se p=d gli intervalli della prospettiva saranno uguali
m=36
for i=0 to m-1
x=p*i/(m-i)
y=k/(x^2+a)
xx= h*x/( d+x) !formula (6): dal PO al PV
yy= d*y/(d+x)
put xx,yy
next i
put h, 0 !punto di fuga
poly2 nsp/2, 1 , get (nsp)
line2 0,k/a,h,0
La curva che è stata utilizzata:
y*(x^2+a)-k=0
è algebrica del terzo ordine. Ha la forma di una campana, con estensione infinita, con y come asse di simmetria. L’asse x è un suo asintoto, i valori delle y sono sempre positivi. Il valore massimo è k/a.
La curva originaria ha in x=0, nel punto di massimo, una tangente orizzontale, ma per effetto della prospettiva la tangente della curva trasformata punta verso la fuga principale (h,0).
La linea inserita serve per verificare che quella è la nuova direzione della tangente.
oggettigeometricigdl 